Programming Project #4 (proj4)
CS180: Intro to Computer Vision and Computational Photography

Neural Radiance Field!

Due Date: November 13th, 2025

Note on compute requirements: We're using PyTorch to implement neural networks with GPU acceleration. If you have an M-series Mac (M1/M2/M3), you should be able to run everything locally using the MPS backend. For older or less powerful hardware, we recommend using GPUs from Colab. Colab Pro is now free for students.

Part 0: Calibrating Your Camera and Capturing a 3D Scan

For the first part of the assignment, you will take a 3D scan of your own object which you will build a NeRF of later! To do this, we will use visual tracking targets called ArUco tags, which provide a way to reliably detect the same 3D keypoints across different images. There are 2 parts: 1) calibrating your camera parameters, and 2) using them to estimate pose. This part can be done entirely locally on your laptop, no need for a GPU. We will be using many helper functions from OpenCV, which you can install with pip install opencv-python.

Part 0.1: Calibrating Your Camera

First, either print out the following calibration tags or pull them up on a laptop/iPad screen. Capture 30-50 images of these tags from your phone camera, keeping the zoom the same. While capturing, results will be best if you vary the angle/distance of the camera, like shown in chessboard calibration in lecture.

Note: For the purpose of this assignment, phone cameras work better since they provide undistorted images without lens effects. If you use a real camera, try to make sure there are no distortion effects.

Now you'll write a script to calibrate your camera using the images you captured. Here's the pipeline:

1. Loop through all your calibration images
2. For each image, detect the ArUco tags using OpenCV's ArUco detector
3. Extract the corner coordinates from the detected tags
4. Collect all detected corners and their corresponding 3D world coordinates (you can consider the ArUco tag as the world origin and define the 4 corners' 3D points relative to that, e.g., if your tag is 0.02m × 0.02m, the corners could be [(0,0,0), (0.02,0,0), (0.02,0.02,0), (0,0.02,0)])
5. Use cv2.calibrateCamera() to compute the camera intrinsics and distortion coefficients

Important: Your code should handle cases where tags aren't detected in some images (this is common). Make sure to check if tags were found before trying to use the detection results, otherwise your script will crash.

Here's a code snippet to get you started with detecting ArUco tags (the tags in the PDF are 4x4):

import cv2
import numpy as np

# Create ArUco dictionary and detector parameters (4x4 tags)
aruco_dict = cv2.aruco.getPredefinedDictionary(cv2.aruco.DICT_4X4_50)
aruco_params = cv2.aruco.DetectorParameters()

# Detect ArUco markers in an image
# Returns: corners (list of numpy arrays), ids (numpy array)
corners, ids, _ = cv2.aruco.detectMarkers(image, aruco_dict, parameters=aruco_params)

# Check if any markers were detected
if ids is not None:
    # Process the detected corners
    # corners: list of length N (number of detected tags)
    #   - each element is a numpy array of shape (1, 4, 2) containing the 4 corner coordinates (x, y)
    # ids: numpy array of shape (N, 1) containing the tag IDs for each detected marker
    # Example: if 3 tags detected, corners will be a list of 3 arrays, ids will be shape (3, 1)
else:
    # No tags detected in this image, skip it
    pass

Part 0.2: Capturing a 3D Object Scan

Next, pick a favorite object of yours, and print out a single ArUco tag, which you can generate from here. Place the object next to the tag on a tabletop, and capture 30-50 images of the object from different angles. Important: Use the same camera and zoom level as you did for calibration. If you cut out the ArUco tag from a piece of paper, make sure to leave a white border around it, otherwise detection will fail.

Capture tips for good quality NeRF results later:

1. Avoid brightness/exposure changes (this is why printing the tag will work better than using a tablet display)
2. Avoid blurry images, try not to introduce motion blur
3. Capture images at varying angles horizontally and vertically
4. Capture images at one uniform distance, about 10-20cm away from the object so that it fills ~50% of the frame

Part 0.3: Estimating Camera Pose

Now that you have calibrated your camera, you can use those intrinsic parameters to estimate the camera pose (position and orientation) for each image of your object. As discussed in lecture, this is the classic Perspective-n-Point (PnP) problem: given a set of 3D points in world coordinates and their corresponding 2D projections in an image, we want to find the camera's extrinsic parameters (rotation and translation).

For each image in your object scan, you'll detect the single ArUco tag and use cv2.solvePnP() to estimate the camera pose. Here's what you need:

Inputs to solvePnP:

• objectPoints (numpy array of shape (N, 3) or (N, 1, 3)): The 3D coordinates of the ArUco tag corners in world space. Since you know the physical size of your printed tag, you can define these coordinates. For example, if your tag is 0.02m × 0.02m, you might define the 4 corners as: [(0,0,0), (0.02,0,0), (0.02,0.02,0), (0,0.02,0)] in meters, with the tag lying flat on the z=0 plane.
• imagePoints (numpy array of shape (N, 2) or (N, 1, 2)): The detected 2D pixel coordinates of the tag corners in the image (from detectMarkers()). You'll need to reshape the corners array from detectMarkers to match this shape.
• cameraMatrix (numpy array of shape (3, 3)): The intrinsic matrix K that you computed in Part 0.1 (contains focal length and principal point)
• distCoeffs (numpy array or None): The distortion coefficients from calibration

Output from solvePnP:

• success (bool): Whether the pose estimation succeeded
• rvec (numpy array of shape (3, 1)): Axis-Angle rotation vector (can be converted to a 3×3 rotation matrix using cv2.Rodrigues())
• tvec (numpy array of shape (3, 1)): Translation vector

Together, the rotation matrix R (from rvec) and translation vector tvec form the camera's extrinsic matrix, which describes where the camera is positioned and oriented relative to the ArUco tag's coordinate system (which we're treating as the world origin). Note: OpenCV's solvePnP() returns the world-to-camera transformation; you will need to invert this to get the camera-to-world (c2w) matrix for visualization and Part 0.4.

Important: Just like in Part 0.1, make sure your code handles cases where the tag isn't detected in some images. You should skip those images rather than letting your code crash.

To help visualize your pose estimation results, you can use the following code snippet to display a camera frustum in 3D (pip install viser):

import viser
import numpy as np

server = viser.ViserServer(share=True)
# Example of visualizing a camera frustum (in practice loop over all images)
# c2w is the camera-to-world transformation matrix (3x4), and K is the camera intrinsic matrix (3x3)
server.scene.add_camera_frustum(
    f"/cameras/{i}", # give it a name
    fov=2 * np.arctan2(H / 2, K[0, 0]), # field of view
    aspect=W / H, # aspect ratio
    scale=0.02, # scale of the camera frustum change if too small/big
    wxyz=viser.transforms.SO3.from_matrix(c2w[:3, :3]).wxyz, # orientation in quaternion format
    position=c2w[:3, 3], # position of the camera
    image=img # image to visualize
)

while True:
    time.sleep(0.1)  # Wait to allow visualization to run

[Deliverables] Include 2 screenshots of your cloud of cameras in Viser showing the camera frustums' poses and images.

Part 0.4: Undistorting images and creating a dataset

Now that you have the camera intrinsics and pose estimates, the final step is to undistort your images and package everything into a dataset format that you can use for training NeRF in the later parts of this project.

First, use cv2.undistort() to remove any lens distortion from your images. This is important because NeRF assumes a perfect pinhole camera model without distortion.

import cv2

# Undistort an image using the calibration results
undistorted_img = cv2.undistort(img, camera_matrix, dist_coeffs)

After undistorting all your images, you'll need to save everything in a .npz file format that matches what's expected for the NeRF training code. You should split your images into training, validation, and test sets, then save using the following keys:

• images_train: numpy array of shape (N_train, H, W, 3) containing your undistorted training images (0-255 range, will be normalized when loaded)
• c2ws_train: numpy array of shape (N_train, 4, 4) containing the camera-to-world transformation matrices for training images
• images_val: numpy array of shape (N_val, H, W, 3) for validation images
• c2ws_val: numpy array of shape (N_val, 4, 4) for validation camera poses
• c2ws_test: numpy array of shape (N_test, 4, 4) for test camera poses (used for novel view rendering)
• focal: float representing the focal length from your camera intrinsics (assuming fx = fy)

You can save your dataset using np.savez():

import numpy as np

# Package your data (keep images in 0-255 range, they'll be normalized when loaded)
np.savez(
    'my_data.npz',
    images_train=images_train,    # (N_train, H, W, 3)
    c2ws_train=c2ws_train,        # (N_train, 4, 4)
    images_val=images_val,        # (N_val, H, W, 3)
    c2ws_val=c2ws_val,            # (N_val, 4, 4)
    c2ws_test=c2ws_test,          # (N_test, 4, 4)
    focal=focal                   # float
)

This dataset can then be loaded in Parts 1 and 2 the same way the provided lego dataset is loaded, allowing you to train a NeRF on your own captured object!

As a sanity check you can test your calibration implementation on our calibration images and our Lafufu dataset which we used to train the NeRF example seen at the end of this project.

Part 1: Fit a Neural Field to a 2D Image

From the lecture we know that we can use a Neural Radiance Field (NeRF) (\(F: \{x, y, z, \theta, \phi\} \rightarrow \{r, g, b, \sigma\}\)) to represent a 3D space. But before jumping into 3D, let's first get familar with NeRF (and PyTorch) using a 2D example. In fact, since there is no concept of radiance in 2D, the Neural Radiance Field falls back to just a Neural Field (\(F: \{u, v\} \rightarrow \{r, g, b\}\)) in 2D, in which \(\{u, v\}\) is the pixel coordinate. In this section, we will create a neural field that can represent a 2D image and optimize that neural field to fit this image. You can start from this image, but feel free to try out any other images.

[Impl: Network] You would need to create an Multilayer Perceptron (MLP) network with Sinusoidal Positional Encoding (PE) that takes in the 2-dim pixel coordinates, and output the 3-dim pixel colors.

• Multilayer Perceptron (MLP): An MLP is simply a stack of non linear activations (e.g., torch.nn.ReLU() or torch.nn.Sigmoid()) and fully connected layers (torch.nn.Linear()). For this part, you can start from building an MLP with the structure shown in the image below. Note that you would need to have a Sigmoid layer at the end of the MLP to constrain the network output be in the range of (0, 1), as a valid pixel color (don't forget to also normalize your image from [0, 255] to [0, 1] when you use it for supervision!). You can take a reference from this tutorial on how to create an MLP in PyTorch.
• Sinusoidal Positional Encoding (PE): PE is an operation that you apply a serious of sinusoidal functions to the input cooridnates, to expand its dimensionality (See equation 4 from this paper for reference). Note we also additionally keep the original input in PE, so the complete formulation is \[PE(x) = \{x, sin(2^0\pi x), cos(2^0\pi x), sin(2^1\pi x), cos(2^1\pi x), ..., sin(2^{L-1}\pi x), cos(2^{L-1}\pi x)\}\] in which \(L\) is the highest frequency level. You can start from \(L=10\) that maps a 2 dimension coordinate to a 42 dimension vector.

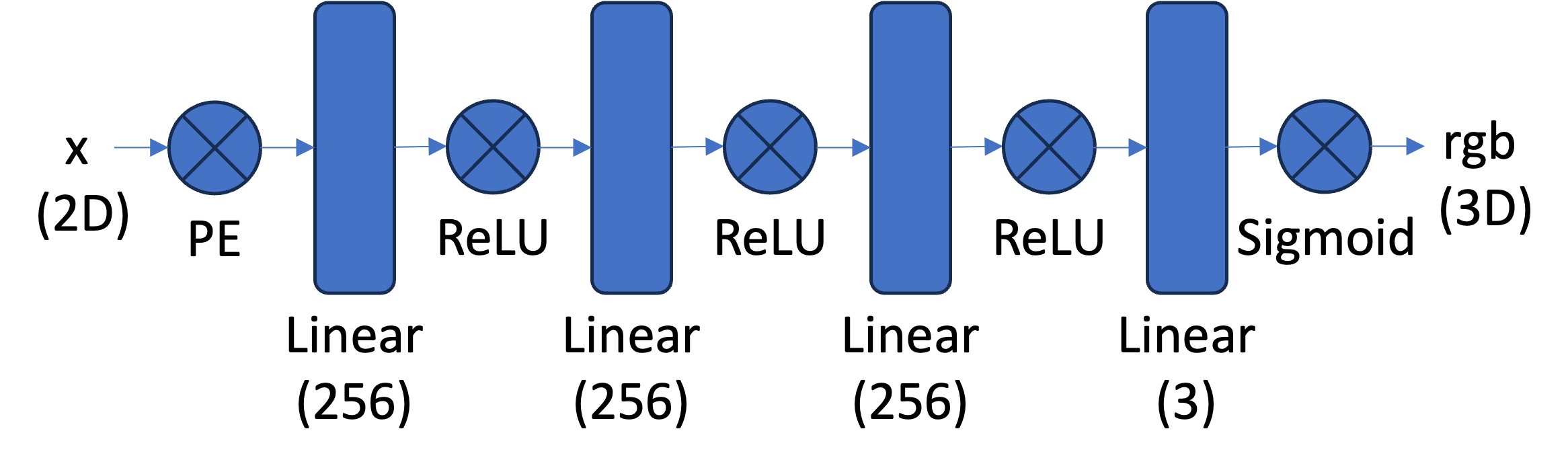
[Impl: Dataloader] If the image is with high resolution, it might be not feasible train the network with the all the pixels in every iteration due to the GPU memory limit. So you need to implement a dataloader that randomly sample \(N\) pixels at every iteration for training. The dataloader is expected to return both the \(N\times2\) 2D coordinates and \(N\times3\) colors of the pixels, which will serve as the input to your network, and the supervision target, respectively (essentially you have a batch size of \(N\)). You would want to normalize both the coordinates (x = x / image_width, y = y / image_height) and the colors (rgbs = rgbs / 255.0) to make them within the range of [0, 1].

[Impl: Loss Function, Optimizer, and Metric] Now that you have the network (MLP) and the dataloader, you need to define the loss function and the optimizer before you can start training your network. You will use mean squared error loss (MSE) (torch.nn.MSELoss) between the predicted color and the groundtruth color. Train your network using Adam (torch.optim.Adam) with a learning rate of 1e-2. Run the training loop for 1000 to 3000 iterations with a batch size of 10k. For the metric, MSE is a good one but it is more common to use Peak signal-to-noise ratio (PSNR) when it comes to measuring the reconstruction quality of a image. If the image is normalized to [0, 1], you can use the following equation to compute PSNR from MSE: \[PSNR = 10 \cdot log_{10}\left(\frac{1}{MSE}\right)\]

[Impl: Hyperparameter Tuning] Vary the layer width (channel size) and the max frequency \(L\) for the positional encoding.

[Deliverables] As a reference, the above images show the process of optimizing the network to fit on this image.

• Report your model architecture including number of layers, width, and learning rate. Feel free to add other details you think are important.
• Show training progression (images at different iterations, similar to the above reference) on both the provided test image and one of your own images.
• Show final results for 2 choices of max positional encoding frequency and 2 choices of width (a 2x2 grid of results). Try very low values for these hyperparameters to see how it affects the outputs.
• Show the PSNR curve for training on one image of your choice.

Part 2: Fit a Neural Radiance Field from Multi-view Images

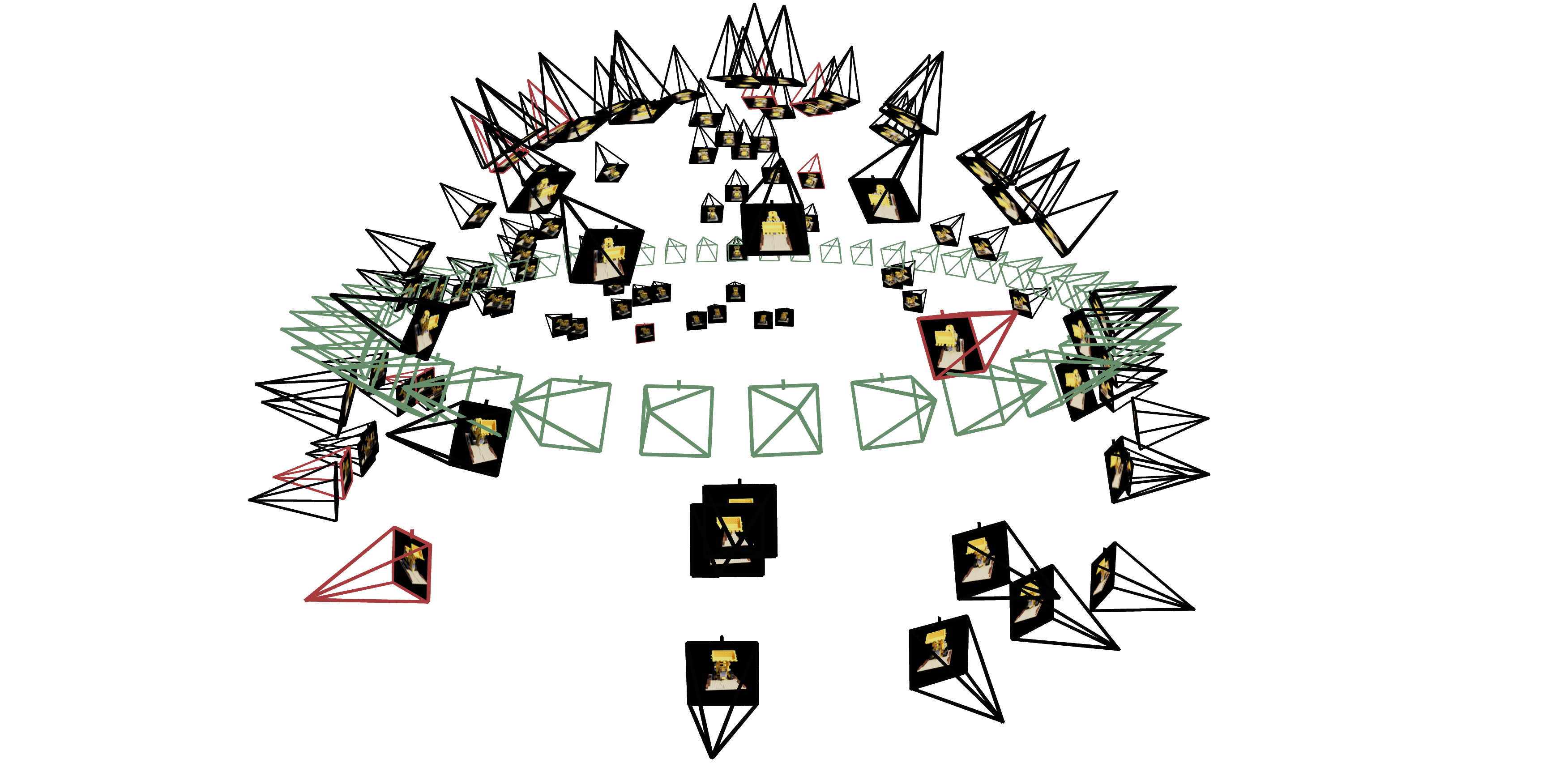
Now that we are familiar with using a neural field to represent a image, we can proceed to a more interesting task that using a neural radiance field to represent a 3D space, through inverse rendering from multi-view calibrated images. For this part we are going to use the Lego scene from the original NeRF paper, but with lower resolution images (200 x 200) and preprocessed cameras (downloaded from here). The following code can be used to parse the data. The figure on its right shows a plot of all the cameras, including training cameras in black, validation cameras in red, and test cameras in green.

data = np.load(f"lego_200x200.npz")

# Training images: [100, 200, 200, 3]
images_train = data["images_train"] / 255.0

# Cameras for the training images 
# (camera-to-world transformation matrix): [100, 4, 4]
c2ws_train = data["c2ws_train"]

# Validation images: 
images_val = data["images_val"] / 255.0

# Cameras for the validation images: [10, 4, 4]
# (camera-to-world transformation matrix): [10, 200, 200, 3]
c2ws_val = data["c2ws_val"]

# Test cameras for novel-view video rendering: 
# (camera-to-world transformation matrix): [60, 4, 4]
c2ws_test = data["c2ws_test"]

# Camera focal length
focal = data["focal"]  # float

Part 2.1: Create Rays from Cameras

Camera to World Coordinate Conversion. The transformation between the world space \(\mathbf{X_w} = (x_w, y_w, z_w)\) and the camera space \(\mathbf{X_c} = (x_c, y_c, z_c)\) can be defined as a rotation matrix \(\mathbf{R}_{3\times3}\) and a translation vector \(\mathbf{t}\): \[\begin{align} \begin{bmatrix} x_c \\ y_c \\ z_c \\ 1 \end{bmatrix} = \begin{bmatrix} \mathbf{R}_{3\times3} & \mathbf{t} \\ \mathbf{0}_{1\times3} & 1 \end{bmatrix} \begin{bmatrix} x_w \\ y_w \\ z_w \\ 1 \end{bmatrix} \end{align}\] in which \(\begin{bmatrix} \mathbf{R}_{3\times3} & \mathbf{t} \\ \mathbf{0}_{1\times3} & 1 \end{bmatrix}\) is called world-to-camera (w2c) transformation matrix, or extrinsic matrix. The inverse of it is called camera-to-world (c2w) transformation matrix.

[Impl] In this session you would need to implement a function x_w = transform(c2w, x_c) that transform a point from camera to the world space. You can verify your implementation by checking if the follow statement is always true: x == transform(c2w.inv(), transform(c2w, x)). Note you might want your implementation to support batched coordinates for later use. You can implement it with either numpy or torch.

Pixel to Camera Coordinate Conversion. Consider a pinhole camera with focal length \((f_x, f_y)\) and principal point \((o_x = \text{image_width} / 2, o_y = \text{image_height} / 2)\), it's intrinsic matrix \(\mathbf{K}\) is defined as: \[\begin{align} \mathbf{K} = \begin{bmatrix} f_x & 0 & o_x \\ 0 & f_y & o_y \\ 0 & 0 & 1 \end{bmatrix} \end{align}\] which can be used to project a 3D point \((x_c, y_c, z_c)\) in the camera coordinate system to a 2D location \((u, v)\) in pixel coordinate system : \[\begin{align} s \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \mathbf{K} \begin{bmatrix} x_c \\ y_c \\ z_c \end{bmatrix} \end{align}\] in which \(s=z_c\) is the depth of this point along the optical axis.

[Impl] In this session you would need to implement a function that invert the aforementioned process, which transform a point from the pixel coordinate system back to the camera coordinate system: x_c = pixel_to_camera(K, uv, s). Similar to the previous session, you might also want your implementation here to support batched coordinates for later use. You can implement it with either numpy or torch.

Pixel to Ray. A ray can be defined by an origin vector \(\mathbf{r}_o \in R^3\) and a direction vector \(\mathbf{r}_d \in R^3\). In the case of a pinhole camera, we want to know the \(\{\mathbf{r}_o, \mathbf{r}_d\}\) for every pixel \((u, v)\). The origin \(\mathbf{r}_o\) of those rays is easy to get because it is just the location of the camera in world coordinates. For a camera-to-world (c2w) transformation matrix \(\begin{bmatrix} \mathbf{R}_{3\times3} & \mathbf{t} \\ \mathbf{0}_{1\times3} & 1 \end{bmatrix}\), the camera origin is simply the translation component: \[\begin{align} \mathbf{r}_o = \mathbf{t} \end{align}\] To calculate the ray direction for pixel \((u, v)\), we can simply choose a point along this ray with depth equal to 1 (\(s=1\)) and find its coordinate in world space \(\mathbf{X_w} = (x_w, y_w, z_w)\) using your previously implemented functions. Then the normalized ray direction can be computed by: \[\begin{align} \mathbf{r}_d = \frac{\mathbf{X_w} - \mathbf{r}_o}{||\mathbf{X_w} - \mathbf{r}_o||_2} \end{align}\]

[Impl] In this section you will need to implement a function that converts a pixel coordinate to a ray with origin and normalized direction: ray_o, ray_d = pixel_to_ray(K, c2w, uv). You might find your previously implemented functions useful here. Similarly, you might also want your implementation to support batched coordinates.

Part 2.2: Sampling

[Impl: Sampling Rays from Images] In Part 1, we have done random sampling on a single image to get the pixel color and pixel coordinates. Here we can build on top of that, and with the camera intrinsics & extrinsics, we would be able to convert the pixel coordinates into ray origins and directions. Make sure to account for the offset from image coordinate to pixel center (this can be done simply by adding .5 to your UV pixel coordinate grid)! Since we have multiple images now, we have two options of sampling rays. Say we want to sample N rays at every training iteration, option 1 is to first sample M images, and then sample N // M rays from every image. The other option is to flatten all pixels from all images and do a global sampling once to get N rays from all images. You can choose which ever way do ray sampling.

[Impl: Sampling Points along Rays.] After having rays, we also need to discritize each ray into samples that live in the 3D space. The simplist way is to uniformly create some samples along the ray (t = np.linspace(near, far, n_samples)). For the lego scene that we have, we can set near=2.0 and far=6.0. The actually 3D corrdinates can be accquired by \(\mathbf{x} = \mathbf{R}_o + \mathbf{R}_d * t\). However this would lead to a fixed set of 3D points, which could potentially lead to overfitting when we train the NeRF later on. On top of this, we want to introduce some small perturbation to the points only during training, so that every location along the ray would be touched upon during training. this can be achieved by something like t = t + (np.random.rand(t.shape) * t_width) where t is set to be the start of each interval. We recommend to set n_samples to 32 or 64 in this project.

Part 2.3: Putting the Dataloading All Together

Similar to Part 1, you would need to write a dataloader that randomly sample pixels from multiview images. What is different with Part 1, is that now you need to convert the pixel coordinates into rays in your dataloader, and return ray origin, ray direction and pixel colors from your dataloader. To verify if you have by far implement everything correctly, we here provide some visualization code to plot the cameras, rays, and samples in 3D. We additionally recommend you try this code with rays sampled only from one camera so you can make sure that all the rays stay within the camera frustum and eliminating the possibility of other smaller harder to catch bugs.

import viser, time  # pip install viser
import numpy as np

# --- You Need to Implement These ------
dataset = RaysData(images_train, K, c2ws_train)
rays_o, rays_d, pixels = dataset.sample_rays(100) # Should expect (B, 3)
points = sample_along_rays(rays_o, rays_d, perturb=True)
H, W = images_train.shape[1:3]
# ---------------------------------------

server = viser.ViserServer(share=True)
for i, (image, c2w) in enumerate(zip(images_train, c2ws_train)):
    server.add_camera_frustum(
        f"/cameras/{i}",
        fov=2 * np.arctan2(H / 2, K[0, 0]),
        aspect=W / H,
        scale=0.15,
        wxyz=viser.transforms.SO3.from_matrix(c2w[:3, :3]).wxyz,
        position=c2w[:3, 3],
        image=image
    )
for i, (o, d) in enumerate(zip(rays_o, rays_d)):
    server.add_spline_catmull_rom(
        f"/rays/{i}", positions=np.stack((o, o + d * 6.0)),
    )
server.add_point_cloud(
    f"/samples",
    colors=np.zeros_like(points).reshape(-1, 3),
    points=points.reshape(-1, 3),
    point_size=0.02,
)

while True:
    time.sleep(0.1)  # Wait to allow visualization to run

# Visualize Cameras, Rays and Samples
import viser, time
import numpy as np

# --- You Need to Implement These ------
dataset = RaysData(images_train, K, c2ws_train)

# This will check that your uvs aren't flipped
uvs_start = 0
uvs_end = 40_000
sample_uvs = dataset.uvs[uvs_start:uvs_end] # These are integer coordinates of widths / heights (xy not yx) of all the pixels in an image
# uvs are array of xy coordinates, so we need to index into the 0th image tensor with [0, height, width], so we need to index with uv[:,1] and then uv[:,0]
assert np.all(images_train[0, sample_uvs[:,1], sample_uvs[:,0]] == dataset.pixels[uvs_start:uvs_end])

# # Uncoment this to display random rays from the first image
# indices = np.random.randint(low=0, high=40_000, size=100)

# # Uncomment this to display random rays from the top left corner of the image
# indices_x = np.random.randint(low=100, high=200, size=100)
# indices_y = np.random.randint(low=0, high=100, size=100)
# indices = indices_x + (indices_y * 200)

data = {"rays_o": dataset.rays_o[indices], "rays_d": dataset.rays_d[indices]}
points = sample_along_rays(data["rays_o"], data["rays_d"], random=True)
# ---------------------------------------

server = viser.ViserServer(share=True)
for i, (image, c2w) in enumerate(zip(images_train, c2ws_train)):
  server.add_camera_frustum(
    f"/cameras/{i}",
    fov=2 * np.arctan2(H / 2, K[0, 0]),
    aspect=W / H,
    scale=0.15,
    wxyz=viser.transforms.SO3.from_matrix(c2w[:3, :3]).wxyz,
    position=c2w[:3, 3],
    image=image
  )
for i, (o, d) in enumerate(zip(data["rays_o"], data["rays_d"])):
  positions = np.stack((o, o + d * 6.0))
  server.add_spline_catmull_rom(
      f"/rays/{i}", positions=positions,
  )
server.add_point_cloud(
    f"/samples",
    colors=np.zeros_like(points).reshape(-1, 3),
    points=points.reshape(-1, 3),
    point_size=0.03,
)

while True:
    time.sleep(0.1)  # Wait to allow visualization to run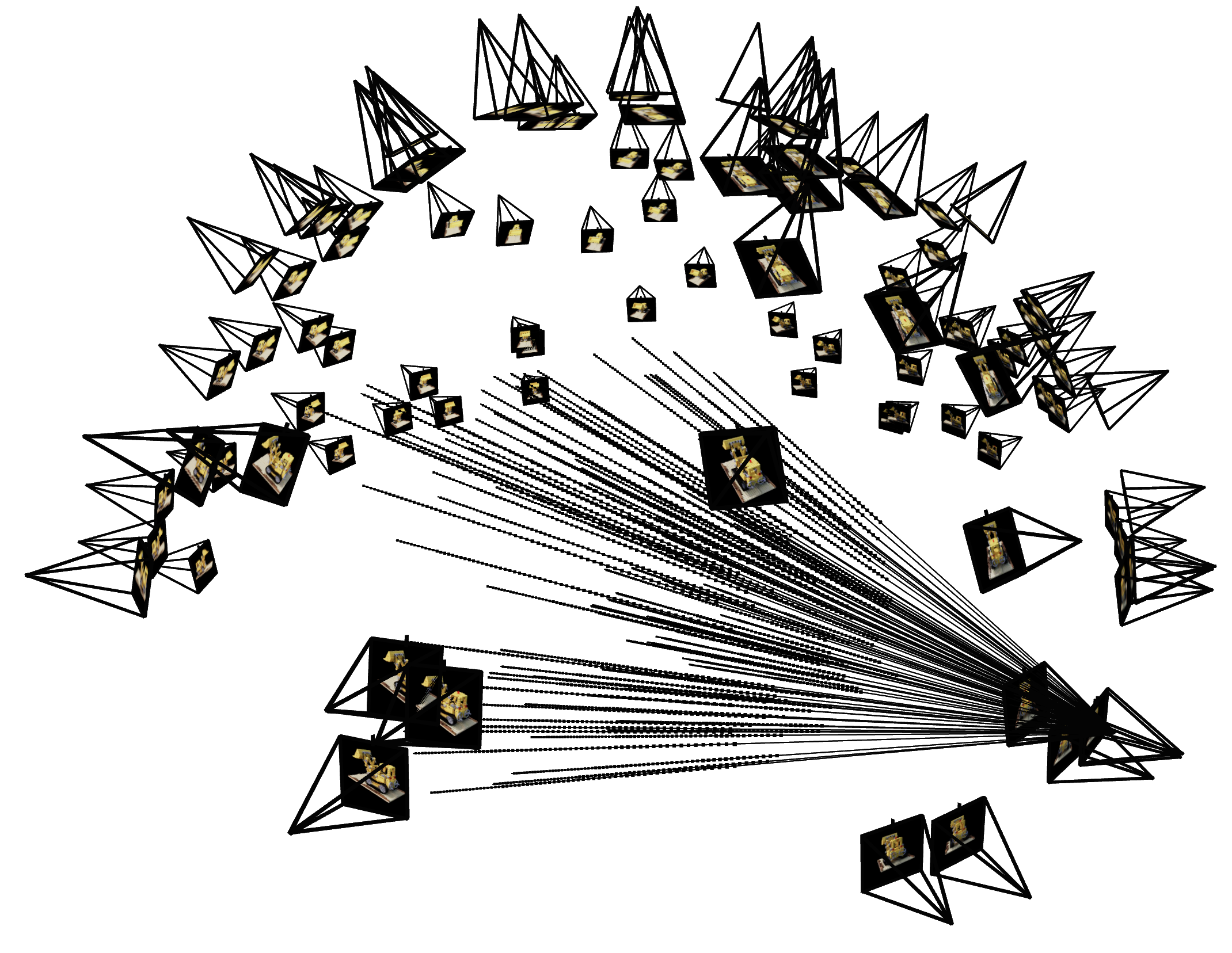

Part 2.4: Neural Radiance Field

[Impl: Network] After having samples in 3D, we want to use the network to predict the density and color for those samples in 3D. So you would create a MLP that is similar to Part 1, but with three changes:

• Input is now 3D world coordinates instead of 2D pixel coordinates, along side a 3D vector as the ray direction. And we are going to output not only the color, but also the density for the 3D points. In the radiance field, the color of each point depends on the view direction, so we are going to use the view direction as the condition when we predict colors. Note we use Sigmoid to constrain the output color within range (0, 1), and use ReLU to constrain the output density to be positive. The ray direction also needs to be encoded by positional encoding (PE) but can use less frequency (e.g., L=4) than the cooridnate PE (e.g., L=10).
• Make the MLP deeper. We are now doing a more challenging task of optimizing a 3D representation instead of 2D. So we need a more powerful network.
• Inject the input (after PE) to the middle of your MLP through concatenation. It's a general trick for deep neural network, that is helpful for it to not forgetting about the input.

Below is a structure of the network that you can start with:

Part 2.5: Volume Rendering

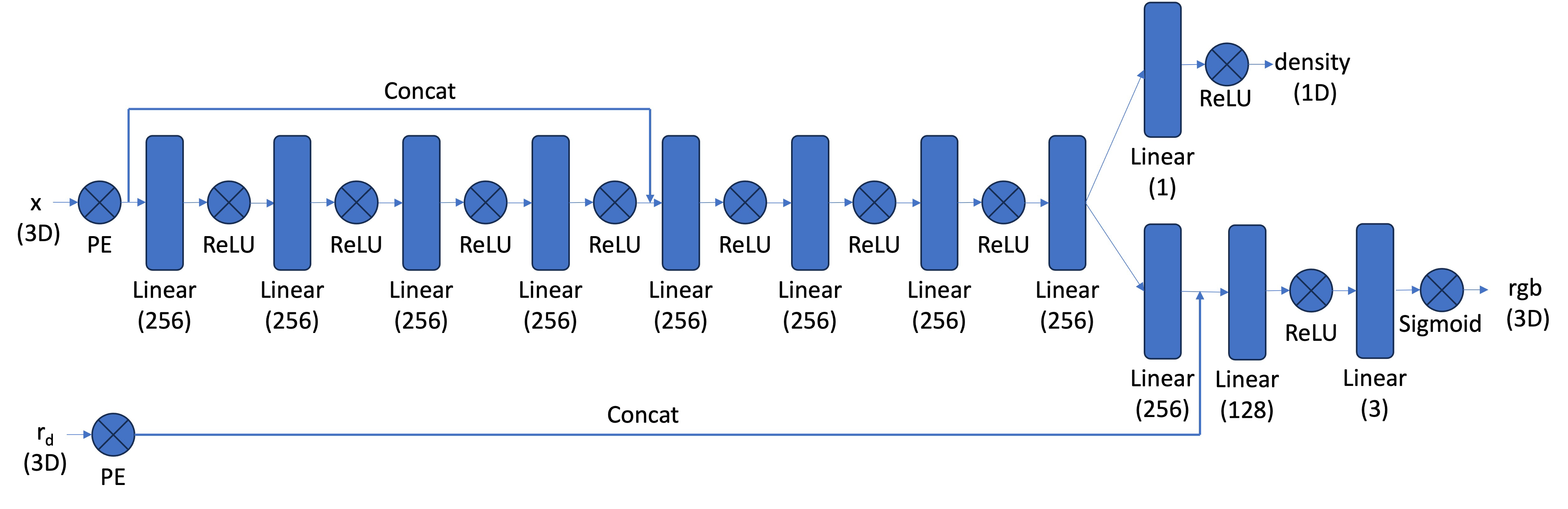
The core volume rendering equation is as follows: \[\begin{align} C(\mathbf{r})=\int_{t_n}^{t_f} T(t) \sigma(\mathbf{r}(t)) \mathbf{c}(\mathbf{r}(t), \mathbf{d}) d t, \text { where } T(t)=\exp \left(-\int_{t_n}^t \sigma(\mathbf{r}(s)) d s\right) \end{align}\]

This fundamentally means that at every small step \(dt\) along the ray, we add the contribution of that small interval \([t, t + dt]\) to that final color, and we do the infinitely many additions if these infintesimally small intervals with an integral.

The discrete approximation (thus tractable to compute) of this equation can be stated as the following: \[\begin{align} \hat{C}(\mathbf{r})=\sum_{i=1}^N T_i\left(1-\exp \left(-\sigma_i \delta_i\right)\right) \mathbf{c}_i, \text { where } T_i=\exp \left(-\sum_{j=1}^{i-1} \sigma_j \delta_j\right) \end{align}\] where \(\textbf{c}_i\) is the color obtained from our network at sample location \(i\), \(T_i\) is the probability of a ray not terminating before sample location \(i\), and \(1 - e^{-\sigma_i \delta_i}\) is the probability of terminating at sample location \(i\).

If your volume rendering works, the following snippet of code should pass the assert statement:

import torch
torch.manual_seed(42)
sigmas = torch.rand((10, 64, 1))
rgbs = torch.rand((10, 64, 3))
step_size = (6.0 - 2.0) / 64
rendered_colors = volrend(sigmas, rgbs, step_size)

correct = torch.tensor([
    [0.5006, 0.3728, 0.4728],
    [0.4322, 0.3559, 0.4134],
    [0.4027, 0.4394, 0.4610],
    [0.4514, 0.3829, 0.4196],
    [0.4002, 0.4599, 0.4103],
    [0.4471, 0.4044, 0.4069],
    [0.4285, 0.4072, 0.3777],
    [0.4152, 0.4190, 0.4361],
    [0.4051, 0.3651, 0.3969],
    [0.3253, 0.3587, 0.4215]
  ])
assert torch.allclose(rendered_colors, correct, rtol=1e-4, atol=1e-4)

[Impl] Here you will implement the volume rendering equation for a batch of samples along a ray. This rendered color is what we will compare with our posed images in order to train our network. You would need to implement this part in torch instead of numpy because we need the loss to be able to backpropagate through this part. A hint is that you may find torch.cumsum or torch.cumprod useful here.

[Deliverables] As a reference, the images below show the process of optimizing the network to fit on our lego multi-view images from a novel view. The staff solution reaches above 23 PSNR with 1000 gradient steps and a batchsize of 10K rays per gradent step. The staff solution uses an Adam optimizer with a learning rate of 5e-4. For guaranteed full credit, achieve 23 PSNR for any number of iterations.

• Include a brief description of how you implement each part.
• Report the visualization of the rays and samples you draw at a single training step (along with the cameras), similar to the plot we show above. Plot up to 100 rays to make it less crowded.
• Visualize the training process by plotting the predicted images across iterations, similar to the above reference, as well as the PSNR curve on the validation set (6 images).
• After you train the network, you can use it to render a novel view image of the lego from arbitrary camera extrinsic. Show a spherical rendering of the lego video using the provided cameras extrinsics (c2ws_test in the npz file). You should be get a video like this (left is 10 after minutes training, right is 2.5 hrs training):

Part 2.6: Training with your own data

You will now use the dataset you created in part 0 to create a NeRF of your chosen object. After training a NeRF on your dataset render a gif of novel views from your scene. We have provided some starter code below which may be useful.

        def look_at_origin(pos):
  # Camera looks towards the origin
  forward = -pos / np.linalg.norm(pos)  # Normalize the direction vector

  # Define up vector (assuming y-up)
  up = np.array([0, 1, 0])

  # Compute right vector using cross product
  right = np.cross(up, forward)
  right = right / np.linalg.norm(right)

  # Recompute up vector to ensure orthogonality
  up = np.cross(forward, right)

  # Create the camera-to-world matrix
  c2w = np.eye(4)
  c2w[:3, 0] = right
  c2w[:3, 1] = up
  c2w[:3, 2] = forward
  c2w[:3, 3] = pos

  return c2w

def rot_x(phi):
    return np.array([
        [math.cos(phi), -math.sin(phi), 0, 0],
        [math.sin(phi), math.cos(phi), 0, 0],
        [0,0,1,0],
        [0,0,0,1],
    ])

# TODO: Change start position to a good position for your scene such as 
# the translation vector of one of your training camera extrinsics
START_POS = np.array([1., 0., 0.])
NUM_SAMPLES = 60

frames = []
for phi in np.linspace(360., 0., NUM_SAMPLES, endpoint=False):
    c2w = look_at_origin(START_POS)
    extrinsic = rot_x(phi/180.*np.pi) @ c2w
    
    # Generate view for this camera pose
    # TODO: Add code for generating a view with your model from the current extrinsic
    frame = ...
    frames.append(frame)
        
      

Helpful Tips / Common Mistakes:

• When using the test data our near and far parameters are set to 2.0 and 6.0 respectively. You will likely have to adjust these for the real data you collect. These parameters represent the minimum and maximum distance away from the camera's sensor that we start and stop sampling. For our example we found that near = 0.02 and far = 0.5 worked well, but you will likely have to do some experimenting to find values that work for you.
• You might want to increase the number of samples along your rays for your real data. This will take longer to train, but can improve visual quality of your NeRF. For our implementation we first trained with 32 samples in order to ensure that there are no issues or bugs in other parts of our code and then increased to 64 samples per ray to get our final result.
• If training is taking an unreasonable amount of time, your image resolution may be the issue. Attempting to train with too large of images may take a long time. If you resize your images you need to ensure that your intrinsics matrix reflects this change either by resizing before doing calibration or adjusting the intrinsics matrix after recovering it.

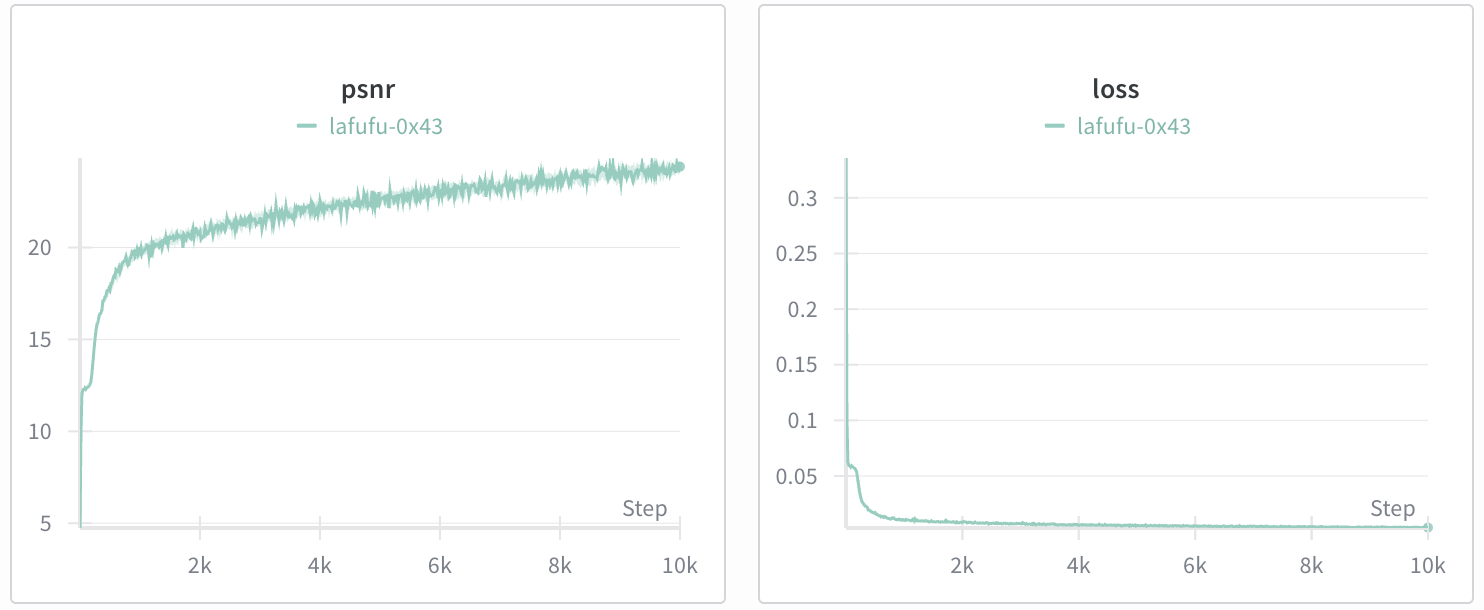
[Impl] Train a NeRF on your chosen object dataset collected in part 0. Make sure to save the training loss over iterations as well as to generate intermediate renders for the deliverables.

[Deliverables] Create a gif of a camera circling the object showing novel views and discuss any code or hyperparameter changes you had to make. Include a plot of the training loss as well as some intermediate renders of the scene while it is training.

Bells & Whistles

Required for CS 280A students only:

• Render the depths map video for the Lego scene. Instead of compositing per-point colors to the pixel color in the volume rendering, we can also composite per-point depths to the pixel depth. (See the reference video below)

Optional for all students:

The following are optional explorations for any students interested in going deeper with NeRF.

• Better (more efficient) sampling: Implement course-to-fine PDF resampling as described in the original NeRF paper.
• Better NeRF representations: Replace MLP with something more advanced to make it faster. (e.g. TensoRF or Instant-NGP). For this part it is ok to borrow some code from existing implementations (mark reference!) to your code base and see how it affect your NeRF optimization.
• Improve PSNR to 30+: Aside from better sampling, better NeRF representations, try other things you can think of to improve the quality of the images to get 30+ db in PSNR.
• Render the Lego video with a different background color than black. You would need to revisit the volume rendering equation to see where you should inject the background color.
• Implement scene contraction for large scenes as specified in Mip-NeRF 360. This allows NeRF to handle unbounded scenes by contracting distant points into a bounded space.
• Use nerfstudio to make a cool video!

Deliverables Checklist

Make sure your submission includes all of the following:

Part 0: Camera Calibration and 3D Scanning

• 2 screenshots of your camera frustums visualization in Viser

Part 1: Fit a Neural Field to a 2D Image

• Model architecture report (number of layers, width, learning rate, and other important details)
• Training progression visualization on both the provided test image and one of your own images
• Final results for 2 choices of max positional encoding frequency and 2 choices of width (2x2 grid)
• PSNR curve for training on one image of your choice

Part 2: Fit a Neural Radiance Field from Multi-view Images

• Brief description of how you implemented each part
• Visualization of rays and samples with cameras (up to 100 rays)
• Training progression visualization with predicted images across iterations
• PSNR curve on the validation set
• Spherical rendering video of the Lego using provided test cameras

Part 2.6: Training with Your Own Data

• GIF of camera circling your object showing novel views
• Discussion of code or hyperparameter changes you made
• Plot of training loss over iterations
• Intermediate renders of the scene during training

Bells & Whistles (if applicable)

• CS 280A students: Depth map video for the Lego scene
• Optional: Any additional explorations you completed