berkeley logo Programming Project #5 (proj5)
CS180: Intro to Computer Vision and Computational Photography
University of California, Berkeley

Flow Matching from Scratch!

For this part, you need to submit your code and website PDF, and also your web url to class gallery via this Google Form.

Due: 12/12/2025 11:59pm

We recommend using GPUs from Colab to finish this project!

Overview

You will train your own flow matching model on MNIST. Starter code can be found in the provided notebook.

START EARLY!

Neural Network Resources

In this part, you will build and train a UNet, which is more complex than the MLP you implemented in the NeRF project. We provide all class definitions you may need in the notebook (but feel free to add or modify them as necessary).

Instead of asking ChatGPT to write everything for you, please consult the following resources when you get stuck — they will help you understand how and why things work under the hood.


Part 1: Training a Single-Step Denoising UNet

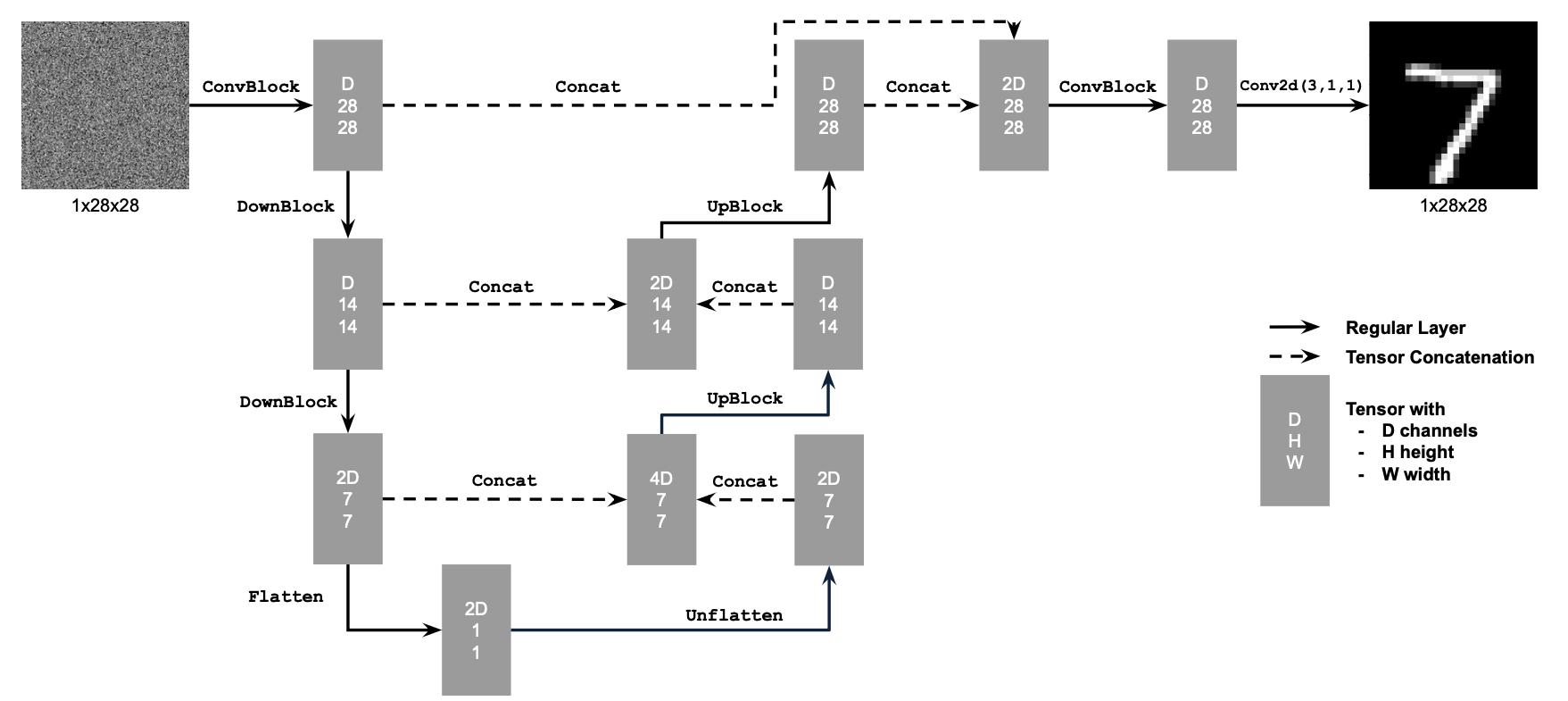
Let's warmup by building a simple one-step denoiser. Given a noisy image $z$, we aim to train a denoiser $D_\theta$ such that it maps $z$ to a clean image $x$. To do so, we can optimize over an L2 loss: $$L = \mathbb{E}_{z,x} \|D_{\theta}(z) - x\|^2 \tag{B.1}$$

1.1 Implementing the UNet

In this project, we implement the denoiser as a UNet. It consists of a few downsampling and upsampling blocks with skip connections.

UNet Architecture

Figure 1: Unconditional UNet

The diagram above uses a number of standard tensor operations defined as follows:

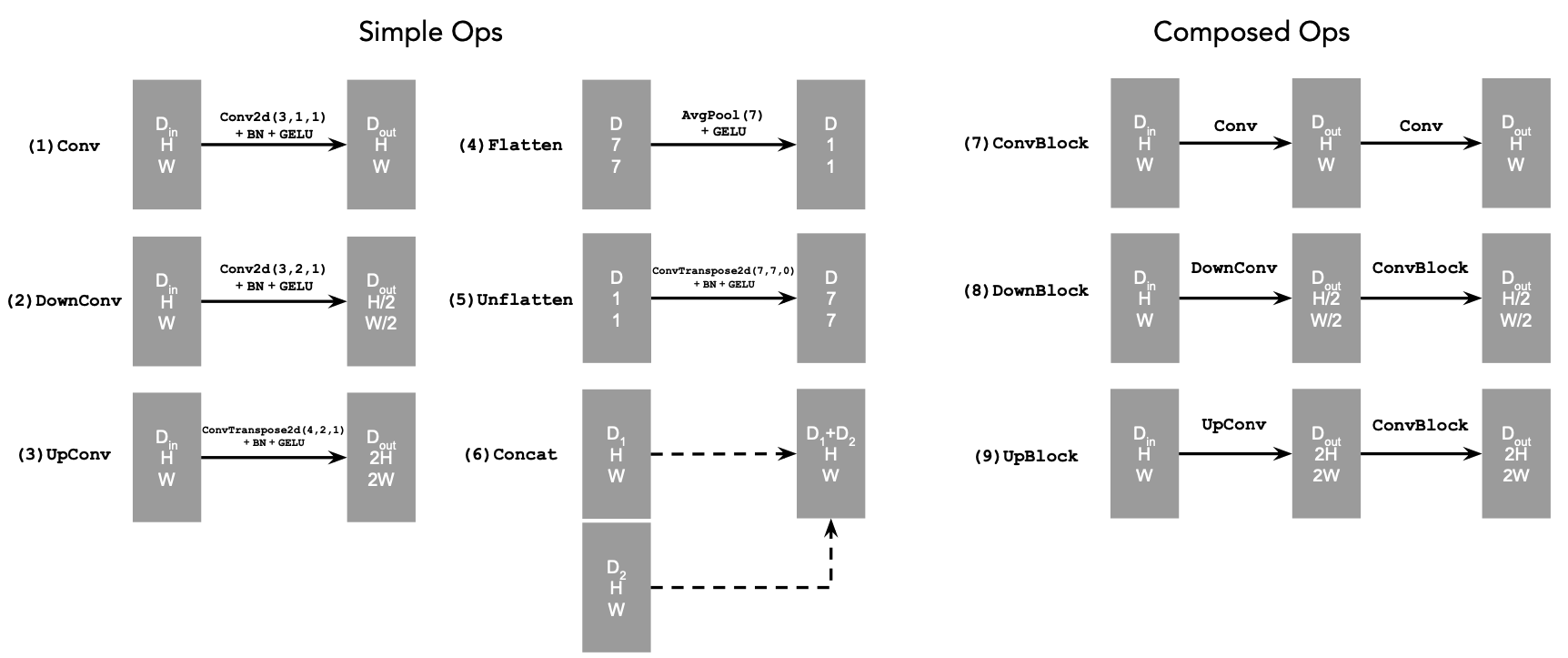
UNet Operations

Figure 2: Standard UNet Operations

where: At a high level, the blocks do the following:

We define composed operations using our simple operations in order to make our network deeper. This doesn't change the tensor's height, width, or number of channels, but simply adds more learnable parameters.

1.2 Using the UNet to Train a Denoiser

Recall from equation 1 that we aim to solve the following denoising problem: Given a noisy image $z$, we aim to train a denoiser $D_\theta$ such that it maps $z$ to a clean image $x$. To do so, we can optimize over an L2 loss $$ L = \mathbb{E}_{z,x} \|D_{\theta}(z) - x\|^2. $$ To train our denoiser, we need to generate training data pairs of ($z$, $x$), where each $x$ is a clean MNIST digit. For each training batch, we can generate $z$ from $x$ using the the following noising process: $$ z = x + \sigma \epsilon,\quad \text{where }\epsilon \sim N(0, I). \tag{B.2} $$ Visualize the different noising processes over $\sigma = [0.0, 0.2, 0.4, 0.5, 0.6, 0.8, 1.0]$, assuming normalized $x \in [0, 1]$. You should see noisier images as $\sigma$ increases.

Deliverable

1.2.1 Training

Now, we will train the model to perform denoising.

You should visualize denoised results on the test set at the end of training. Display sample results after the 1st and 5th epoch.

After 5 epoch training, they should look something like these:

After the 5-th epoch

Figure 3: Results on digits from the test set after 5 epochs of training

Deliverables

1.2.2 Out-of-Distribution Testing

Our denoiser was trained on MNIST digits noised with $\sigma = 0.5$. Let's see how the denoiser performs on different $\sigma$'s that it wasn't trained for.

Visualize the denoiser results on test set digits with varying levels of noise $\sigma = [0.0, 0.2, 0.4, 0.5, 0.6, 0.8, 1.0]$.

Deliverables

1.2.3 Denoising Pure Noise

To make denoising a generative task, we'd like to be able to denoise pure, random Gaussian noise. We can think of this as starting with a blank canvas $z = \epsilon$ where $\epsilon \sim N(0, I)$ and denoising it to get a clean image $x$.

Repeat the same training process as in part 1.2.1, but input pure noise $\epsilon \sim N(0, I)$ and denoise it for 5 epochs. Display your results after 1 and 5 epochs.

Sample from the denoiser that was trained to denoise pure noise. What patterns do you observe in the generated outputs? What relationship, if any, do these outputs have with the training images (e.g., digits 0–9)? Why might this be happening?

Deliverables

Hint

Part 2: Training a Flow Matching Model

We just saw that one-step denoising does not work well for generative tasks. Instead, we need to iteratively denoise the image, and we will do so with flow matching. Here, we will iteratively denoise an image by training a UNet model to predict the `flow' from our noisy data to clean data. In our flow matching setup, we sample a pure noise image $x_0 \sim \mathcal{N}(0, I)$ and generate a realistic image $x_1$.

For iterative denoising, we need to define how intermediate noisy samples are constructed. The simplest approach would be a linear interpolation between noisy $x_0$ and clean $x_1$ for some $x_1$ in our training data:

\begin{equation} x_t = (1-t)x_0 + tx_1 \quad \text{where } x_0 \sim \mathcal{N}(0, 1), t \in [0, 1]. \tag{B.3} \end{equation} This is a vector field describing the position of a point $x_t$ at time $t$ relative to the clean data distribution $p_1(x_1)$ and the noisy data distribution $p_0(x_0)$. Intuitively, we see that for small $t$, we remain close to noise, while for larger $t$, we approach the clean distribution.

Flow can be thought of as the velocity (change in posiiton w.r.t. time) of this vector field, describing how to move from $x_0$ to $x_1$: \begin{equation} u(x_t, t) = \frac{d}{dt} x_t = x_1 - x_0. \tag{B.4}\end{equation}

Our aim is to learn a UNet $u_\theta(x_t,t)$ which approximates this flow $u(x_t, t) = x_1 - x_0$, giving us our learning objective: \begin{equation} L = \mathbb{E}_{x_0 \sim p_0(x_0), x_1 \sim p_1(x_1), t \sim U[0, 1]} \|(x_1-x_0) - u_\theta(x_t, t)\|^2. \tag{B.5} \end{equation}

2.1 Adding Time Conditioning to UNet

We need a way to inject scalar $t$ into our UNet model to condition it. There are many ways to do this. Here is what we suggest:
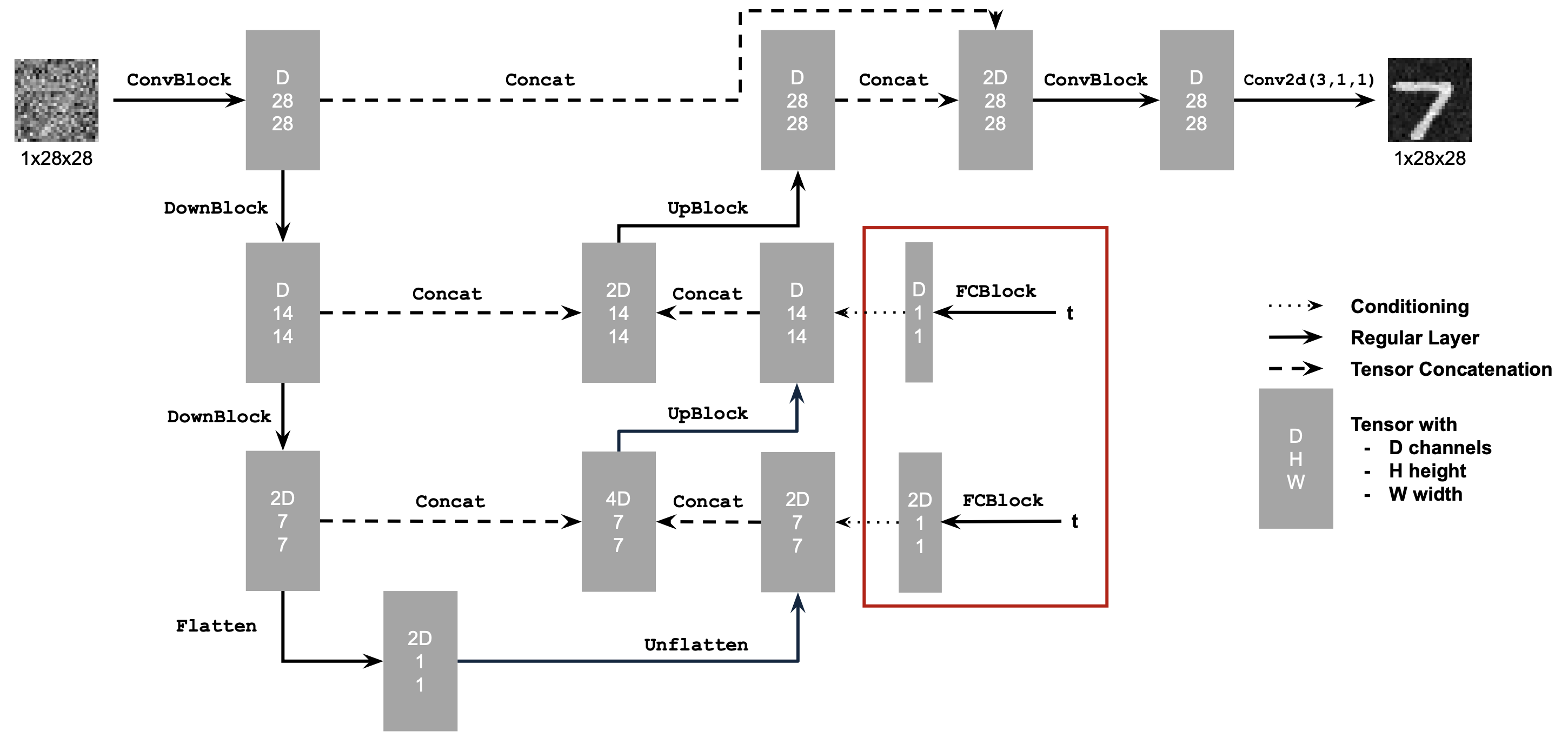
UNet Highlighted

Figure 4: Conditioned UNet

Note: It may look like we're predicting the original image in the figure above, but we are not. We're predicting the flow from the noisy $x_0$ to clean $x_1$, which will contain both parts of the original image as well as the noise to remove.

This uses a new operator called FCBlock (fully-connected block) which we use to inject the conditioning signal into the UNet:

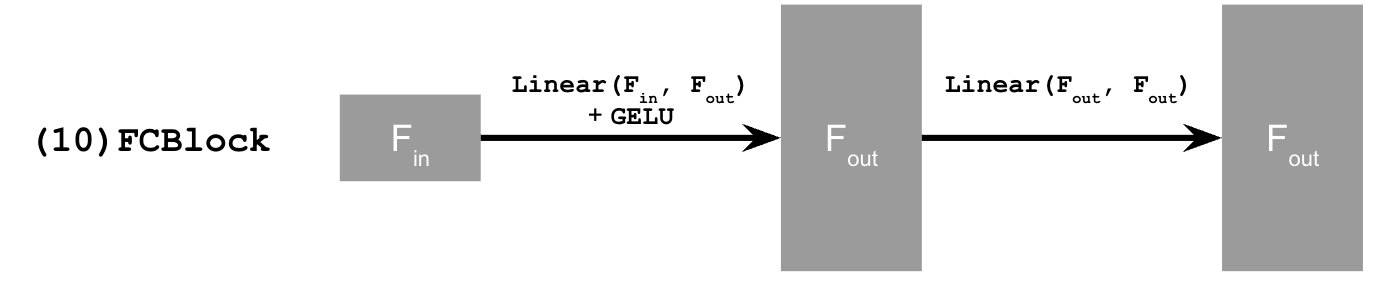
FCBlock

Figure 5: FCBlock for conditioning

Here Linear(F_in, F_out) is a linear layer with F_in input features and F_out output features. You can implement it using nn.Linear.

Since our conditioning signal $t$ is a scalar, F_in should be of size 1.

You can embed $t$ by following this pseudo code: 


fc1_t = FCBlock(...)
fc2_t = FCBlock(...)

# the t passed in here should be normalized to be in the range [0, 1]
t1 = fc1_t(t)
t2 = fc2_t(t)

# Follow diagram to get unflatten.
# Replace the original unflatten with modulated unflatten.
unflatten = unflatten * t1
# Follow diagram to get up1.
...
# Replace the original up1 with modulated up1.
up1 = up1 * t2
# Follow diagram to get the output.
...

2.2 Training the UNet

Training our time-conditioned UNet $u_\theta(x_t, t)$ is now pretty easy. Basically, we pick a random image $x_1$ from the training set, a random timestep $t$, add noise to $x_1$ to get $x_t$, and train the denoiser to predict the flow at $x_t$. We repeat this for different images and different timesteps until the model converges and we are happy.

Algorithm Diagram

Algorithm B.1. Training time-conditioned UNet

Deliverable

2.3 Sampling from the UNet

We can now use our UNet for iterative denoising using the algorithm below! The results would not be perfect, but legible digits should emerge

Algorithm Diagram

Algorithm B.2. Sampling from time-conditioned UNet

Epoch 1

Epoch 10

Deliverables

2.4 Adding Class-Conditioning to UNet

To make the results better and give us more control for image generation, we can also optionally condition our UNet on the class of the digit 0-9. This will require adding 2 more FCBlocks to our UNet but, we suggest that for class-conditioning vector $c$, you make it a one-hot vector instead of a single scalar. Because we still want our UNet to work without it being conditioned on the class (recall the classifer-free guidance you implemented in part a), we implement dropout where 10% of the time ($p_{\text{uncond}}= 0.1$) we drop the class conditioning vector $c$ by setting it to 0. Here is one way to condition our UNet $u_\theta(x_t, t, c)$ on both time $t$ and class $c$: 

fc1_t = FCBlock(...)
fc1_c = FCBlock(...)
fc2_t = FCBlock(...)
fc2_c = FCBlock(...)

t1 = fc1_t(t)
c1 = fc1_c(c)
t2 = fc2_t(t)
c2 = fc2_c(c)

# Follow diagram to get unflatten.
# Replace the original unflatten with modulated unflatten.
unflatten = c1 * unflatten + t1
# Follow diagram to get up1.
...
# Replace the original up1 with modulated up1.
up1 = c2 * up1 + t2
# Follow diagram to get the output.
...

2.5 Training the UNet

Training for this section will be the same as time-only, with the only difference being the conditioning vector $c$ and doing unconditional generation periodically.


Algorithm Diagram

Algorithm B.3. Training class-conditioned UNet

Deliverable

2.6 Sampling from the UNet

Now we will sample with class-conditioning and will use classifier-free guidance with $\gamma = 5.0$.

Algorithm Diagram

Algorithm B.4. Sampling from class-conditioned UNet

Epoch 1

Epoch 10

Deliverables

Part 3: Bells & Whistles

Required for CS280A students only: Optional for all students:

Deliverable Checklist

Acknowledgements

This project was a joint effort by Ryan Tabrizi, Daniel Geng, Hang Gao, and Jingfeng Yang, advised by Liyue Shen, Andrew Owens, Angjoo Kanazawa, and Alexei Efros. We also thank David McAllister and Songwei Ge for their helpful feedback and suggestions.